TEORIAS E FILOSOFIAS DE GRACELI 135+
- Gerar link
- X
- Outros aplicativos
carga elétrica quântica e entropia no sistema decadimensional e categorial Graceli
terça-feira, 22 de janeiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Carga elétrica (AO 1945: carga eléctrica) é uma propriedade física fundamental que determina as interações eletromagnéticas. Esta carga está armazenada em grande quantidade nos corpos ao nosso redor, mas a percepção dela não ocorre facilmente. Convenciona-se a existência de dois tipos de carga, a positiva e a negativa, que, em equilíbrio, são imperceptíveis. Quando há tal igualdade ou equilíbrio de cargas num corpo, diz-se que está eletricamente neutro, ou seja, está sem nenhuma carga líquida para interagir com outros corpos. Um corpo está carregado eletricamente quando possui uma pequena quantidade de carga desequilibrada ou carga líquida. Objetos carregados eletricamente interagem exercendo forças, de atração ou repulsão, uns sobre os outros. A unidade de medida da grandeza carga elétrica no Sistema Internacional de Unidades é o coulomb, representado por C, que recebeu este nome em homenagem ao físico francês Charles Augustin de Coulomb.[1]
Entre partículas elétricas existem forças gravitacionais de atração devido às suas massas e forças elétricas devidas às suas cargas elétricas. Nesse caso, as forças gravitacionais podem ser desprezadas, visto que a massa de uma partícula é ínfima. A força gravitacional só é perceptível quando há a interação entre corpo de massas de grandes proporções, como a Terra e a Lua, por exemplo.
Os átomos são constituídos por prótons, elétrons e nêutrons. Os prótons e os elétrons possuem cargas elétricas iguais em módulo, enquanto que os nêutrons e os fótons são eletricamente neutros. Por mera convenção define-se que os prótons possuem uma carga elétrica elementar de uma unidade positiva, representada por +e, e também que os elétrons têm uma carga elétrica negativa, expressa por -e.
Quantização da carga. Nas colisões entre partículas a altas energias são produzidas muitas outras novas partículas, diferentes dos eletrões, protões e neutrões. Todas as partículas observadas têm sempre uma carga que é um múltiplo inteiro da carga elementar  Assim, a carga de qualquer objeto é sempre um múltiplo inteiro da carga elementar.
Assim, a carga de qualquer objeto é sempre um múltiplo inteiro da carga elementar.
 Assim, a carga de qualquer objeto é sempre um múltiplo inteiro da carga elementar.
Assim, a carga de qualquer objeto é sempre um múltiplo inteiro da carga elementar.Nas experiências de eletrostática, as cargas produzidas são normalmente equivalentes a um número muito elevado de cargas elementares. Por tanto, nesse caso é uma boa aproximação admitir que a carga varia continuamente e não de forma discreta.
Conservação da carga. Em qualquer processo, a carga total inicial é igual à carga total final. Nos casos dos fenómenos em que existe transferência de eletrões entre os átomos, a conservação de carga é evidente. Mas nos casos de criação de novas partículas não teria que ser assim, de facto em todos os processos observados nos raios cósmicos, e nos aceleradores de partículas, existe sempre conservação da carga, ou seja, sempre que uma nova partícula é criada, é também criada uma outra partícula com carga simétrica.
Lei de Coulomb
Essa lei estabelece que "a força de atração ou repulsão entre dois corpos carregados é diretamente proporcional ao produto de suas cargas e inversamente proporcional ao quadrado da distância".[2] Pela lei de Coulomb, duas cargas elétricas pontuais de 1 coulomb separadas de um metro exercem uma sobre a outra uma força de 9 × 109 N, isto é, aproximadamente o peso de 900 000 toneladas. O coulomb é, portanto, uma unidade de ordem de grandeza elevada para exprimir quantidades de cargas estáticas e utilizam-se geralmente seus sub-múltiplos microcoulomb (μC) ou nanocoulomb (nC).
Outras unidades de medida de carga elétrica, usadas em situações especiais, são:
- Carga elementar (e);
- Ampère-hora (Ah);
- Abcoulomb (AbC);
- Statcoulomb (StC).
Força entre cargas[editar | editar código-fonte]
No século XVIII Benjamin Franklin descobriu que as cargas elétricas colocadas na superfície de um objeto metálico podem produzir forças elétricas elevadas nos corpos no exterior do objeto, mas não produzem nenhuma força nos corpos colocados no interior.
No século anterior Isaac Newton já tinha demonstrado de forma analítica que a força gravítica produzida por uma casca oca é nula no seu interior. Esse resultado é consequência da forma como a força gravítica entre partículas diminui em função do quadrado da distância.[3]
Concluiu então Franklin que a força elétrica entre partículas com carga deveria ser também proporcional ao inverso do quadrado da distância entre as partículas. No entanto, uma diferença importante entre as forças elétrica e gravítica é que a força gravítica é sempre atrativa, enquanto que a força elétrica pode ser atrativa ou repulsiva:
- A força elétrica entre duas cargas com o mesmo sinal é repulsiva.
- A força elétrica entre duas cargas com sinais opostos é atrativa.
Vários anos após o trabalho de Franklin, Charles de Coulomb fez experiências para estudar com precisão o módulo da força eletrostática entre duas cargas pontuais.
Uma carga pontual é uma distribuição de cargas numa pequena região do espaço.
A lei de Coulomb estabelece que o módulo da força elétrica entre duas cargas pontuais é diretamente proporcional ao valor absoluto de cada uma das cargas, e inversamente proporcional à distância ao quadrado

onde  é a distância entre as cargas,
é a distância entre as cargas,  e
e  são as cargas das duas partículas,
são as cargas das duas partículas,  é uma constante de proporcionalidade designada de constante de Coulomb, e
é uma constante de proporcionalidade designada de constante de Coulomb, e  é a constante dielétrica do meio que existir entre as duas cargas. A constante dielétrica do vácuo é exatamente igual a 1, e a constante do ar é muito próxima desse valor; assim, se entre as cargas existir ar,
é a constante dielétrica do meio que existir entre as duas cargas. A constante dielétrica do vácuo é exatamente igual a 1, e a constante do ar é muito próxima desse valor; assim, se entre as cargas existir ar,  pode ser eliminada na equação.[4]
pode ser eliminada na equação.[4]
 é a distância entre as cargas,
é a distância entre as cargas,  e
e  são as cargas das duas partículas,
são as cargas das duas partículas,  é uma constante de proporcionalidade designada de constante de Coulomb, e
é uma constante de proporcionalidade designada de constante de Coulomb, e  é a constante dielétrica do meio que existir entre as duas cargas. A constante dielétrica do vácuo é exatamente igual a 1, e a constante do ar é muito próxima desse valor; assim, se entre as cargas existir ar,
é a constante dielétrica do meio que existir entre as duas cargas. A constante dielétrica do vácuo é exatamente igual a 1, e a constante do ar é muito próxima desse valor; assim, se entre as cargas existir ar,  pode ser eliminada na equação.[4]
pode ser eliminada na equação.[4]No sistema internacional de unidades, o valor da constante de Coulomb é:

Outros meios diferentes do ar têm constantes dielétricas K sempre maiores que o ar; consequentemente, a força elétrica será mais fraca se as cargas pontuais forem colocadas dentro de um meio diferente do ar.[4]
Campo elétrico[editar | editar código-fonte]
Uma forma diferente de explicar a força eletrostática entre duas partículas com carga consiste em admitir que cada carga elétrica cria à sua volta um campo que atua sobre outras partículas com carga. Se colocarmos uma partícula com carga  num ponto onde existe um campo elétrico, o resultado será uma força elétrica
num ponto onde existe um campo elétrico, o resultado será uma força elétrica  ; o campo elétrico
; o campo elétrico  define-se como a força por unidade de carga:[5]
define-se como a força por unidade de carga:[5]
 num ponto onde existe um campo elétrico, o resultado será uma força elétrica
num ponto onde existe um campo elétrico, o resultado será uma força elétrica  ; o campo elétrico
; o campo elétrico  define-se como a força por unidade de carga:[5]
define-se como a força por unidade de carga:[5]
Consequentemente, o campo elétrico num ponto é um vetor que indica a direção e o sentido da força elétrica que sentiria uma carga unitária positiva colocada nesse ponto.
De forma inversa, se soubermos que num ponto existe um campo elétrico  , podemos calcular facilmente a força elétrica que atua sobre uma partícula com carga
, podemos calcular facilmente a força elétrica que atua sobre uma partícula com carga  , colocada nesse sítio: a força será
, colocada nesse sítio: a força será  . Precisamos apenas de conhecer o campo para calcular a força; não temos de saber quais são as cargas que deram origem a esse campo. [4] No sistema SI, o campo elétrico tem unidades de newton sobre coulomb (N/C).
. Precisamos apenas de conhecer o campo para calcular a força; não temos de saber quais são as cargas que deram origem a esse campo. [4] No sistema SI, o campo elétrico tem unidades de newton sobre coulomb (N/C).
 , podemos calcular facilmente a força elétrica que atua sobre uma partícula com carga
, podemos calcular facilmente a força elétrica que atua sobre uma partícula com carga  , colocada nesse sítio: a força será
, colocada nesse sítio: a força será  . Precisamos apenas de conhecer o campo para calcular a força; não temos de saber quais são as cargas que deram origem a esse campo. [4] No sistema SI, o campo elétrico tem unidades de newton sobre coulomb (N/C).
. Precisamos apenas de conhecer o campo para calcular a força; não temos de saber quais são as cargas que deram origem a esse campo. [4] No sistema SI, o campo elétrico tem unidades de newton sobre coulomb (N/C).Como vimos, a força elétrica produzida por uma carga pontual positiva  sobre uma segunda carga de prova
sobre uma segunda carga de prova  positiva é sempre uma força repulsiva, com módulo que diminui proporcionalmente ao quadrado da distância. Assim, O campo elétrico produzido por uma carga pontual positiva
positiva é sempre uma força repulsiva, com módulo que diminui proporcionalmente ao quadrado da distância. Assim, O campo elétrico produzido por uma carga pontual positiva  são vetores com direção e sentido a afastar-se da carga, como se mostra no lado esquerdo da figura ao lado.
são vetores com direção e sentido a afastar-se da carga, como se mostra no lado esquerdo da figura ao lado.
 sobre uma segunda carga de prova
sobre uma segunda carga de prova  positiva é sempre uma força repulsiva, com módulo que diminui proporcionalmente ao quadrado da distância. Assim, O campo elétrico produzido por uma carga pontual positiva
positiva é sempre uma força repulsiva, com módulo que diminui proporcionalmente ao quadrado da distância. Assim, O campo elétrico produzido por uma carga pontual positiva  são vetores com direção e sentido a afastar-se da carga, como se mostra no lado esquerdo da figura ao lado.
são vetores com direção e sentido a afastar-se da carga, como se mostra no lado esquerdo da figura ao lado.Uma forma mais conveniente de representar esse campo vetorial consiste em desenhar alguma linhas de campo, como foi feito no lado direito da figura anterior. Em cada ponto, a linha de campo que passa por esse ponto aponta na direção do campo. O módulo do campo é maior nas regiões onde as linhas de campo estão mais perto umas das outras.[4]
Para calcular o valor do campo elétrico produzido pela carga pontual  num ponto, coloca-se uma carga de prova
num ponto, coloca-se uma carga de prova  nesse ponto e divide-se a força elétrica pela carga
nesse ponto e divide-se a força elétrica pela carga  . Usando a lei de Coulomb, obtemos o módulo do campo elétrico produzido pela carga
. Usando a lei de Coulomb, obtemos o módulo do campo elétrico produzido pela carga  :
:
 num ponto, coloca-se uma carga de prova
num ponto, coloca-se uma carga de prova  nesse ponto e divide-se a força elétrica pela carga
nesse ponto e divide-se a força elétrica pela carga  . Usando a lei de Coulomb, obtemos o módulo do campo elétrico produzido pela carga
. Usando a lei de Coulomb, obtemos o módulo do campo elétrico produzido pela carga  :
:
onde  é a distância desde a carga
é a distância desde a carga  , que produz o campo, até o ponto onde se calcula o campo. O sinal da carga
, que produz o campo, até o ponto onde se calcula o campo. O sinal da carga  indicará se o campo é repulsivo
indicará se o campo é repulsivo  ou atrativo
ou atrativo  .
.
 é a distância desde a carga
é a distância desde a carga  , que produz o campo, até o ponto onde se calcula o campo. O sinal da carga
, que produz o campo, até o ponto onde se calcula o campo. O sinal da carga  indicará se o campo é repulsivo
indicará se o campo é repulsivo  ou atrativo
ou atrativo  .
.O campo elétrico criado por uma única carga pontual é muito fraco para ser observado. Os campos que observamos mais facilmente são criados por muitas cargas; seria preciso somar vetorialmente todos os campos de cada carga para obter o campo total.[4]
As linhas de campo elétrico produzidas por um sistema de muitas cargas já não serão retas, como na figura anterior, mas poderão ser curvas.
Carga por indução[editar | editar código-fonte]
Um método usado para carregar dois condutores isolados, ficando com cargas idênticas mas de sinais opostos, é o método de carga por indução ilustrado na figura. Os dois condutores isolados são colocados em contato. A seguir aproxima-se um objeto carregado, como se mostra na figura abaixo. O campo elétricoproduzido pelo objeto carregado induz uma carga de sinal oposto no condutor que estiver mais próximo, e uma carga do mesmo sinal no condutor que estiver mais afastado. [4]
A seguir, separam-se os dois condutores mantendo o objeto carregado na mesma posição. Finalmente, retira-se o objeto carregado, ficando os dois condutores carregados com cargas opostas; em cada condutor as cargas distribuem-se pela superfície, devido à repulsão entre elas, mas as cargas dos dois condutores já não podem recombinar-se por não existir contato entre eles.
Na máquina de Wimshurst, usa-se esse método para separar cargas de sinais opostos. Os condutores que entram em contato são duas pequenas lâminas metálicas diametralmente opostas sobre um disco isolador, quando passam por duas escovas metálicas ligadas a uma barra metálica.[4]
As duas lâminas permanecem em contato apenas por alguns instantes, devido a que o disco roda. Se no momento em que duas das lâminas de um disco entram em contato uma lâmina do disco oposto estiver carregada, essa carga induzirá cargas de sinais opostos nas duas lâminas que entraram em contato. Essas cargas opostas induzidas em duas regiões do disco induzem também cargas no disco oposto, porque nesse disco também há uma barra que liga temporariamente as lâminas diametralmente opostas.
Em cada disco, após induzirem cargas no disco oposto, as cargas saltam para dois coletores ligados a duas garrafas metálicas; uma das garrafas armazena carga positiva e a outra carga negativa. Quando as cargas acumuladas nas garrafas forem elevadas produz-se uma descarga elétrica entre as pontas de duas barras ligadas às garrafas, ficando descarregadas. Essa descarga elétrica é um pequeno trovão com uma faísca bastante luminosa.[4]
Os dois discos rodam em sentidos opostos e as duas barras que estabelecem o contato em cada disco e os dois coletores estão colocados de forma a que na rotação de cada lâmina no disco, primeiro seja induzida uma carga que a seguir induz carga oposta no disco oposto e logo passe para o coletor, ficando descarregada e pronta para iniciar outro ciclo.
A cada ciclo as cargas induzidas aumentam, porque cada lâmina é induzida pelas cargas de várias lâminas no disco oposto. Para iniciar o processo basta com que uma das lâminas tenha acumulado alguma pequena carga por contato com outro corpo como, por exemplo, o ar à volta. A localização inicial dessa lâmina com carga determinará qual das garrafas acumula carga positiva e qual negativa.[4]
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.

x

 = entropia reversível
= entropia reversível

x

 = entropia reversível
= entropia reversível

x

 = entropia reversível
= entropia reversível

x

 = entropia reversível
= entropia reversível

x

 = entropia reversível
= entropia reversível

x

 = entropia reversível
= entropia reversível

x

 = entropia reversível
= entropia reversível
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
ferromagnetismo no sistema decadimensional e categorial Graceli
quinta-feira, 24 de janeiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Logo:
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD - Abaixo da qual se manifestam os efeitos do ferromagnetismo. As quantidades “s” e “k” são os autovalores do spin e a constante de Boltzmann repectivamente, enquanto
é dado por:
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
Historicamente, o termo ferromagnético foi usado para qualquer material que exibisse magnetização espontânea, i.e, um momento magnético na ausência de um campo magnético externo. Esta definição geral é ainda de uso comum. Mais recentemente, no entanto, diferentes classes de magnetização espontânea foram identificadas. Em particular, um material é ferromagnético somente se todos os seus íons magnéticos adicionarem uma contribuição positiva para a magnetização líquida. Se alguns dos íons magnéticos subtrair a magnetização líquida (se forem parcialmente antialinhados), então o material é ferrimagnético. Se os momentos dos íons alinhados e antialinhados forem iguais, de modo a ter magnetização líquida zero, apesar do ordenamento magnético, então o material é um antiferromagneto. Estes efeitos de alinhamento só ocorrem em temperaturas abaixo de uma determinada temperatura crítica, denominada temperatura Curie (para ferromagnetos e ferrimagnetos) ou a temperatura Néel (para antiferromagneto).
Ciclo de histerese[editar | editar código-fonte]
Quando um campo magnético externo é aplicado a um ferromagneto como o ferro, os dipolos atômicos irão alinhar-se com ele. Mesmo quando o campo é removido, parte do alinhamento vai ser mantido: o material tornou-se magnetizado. Uma vez magnetizado, o imã vai ficar magnetizado por tempo indeterminado. Para desmagnetizar exige-se aplicação de calor ou de um campo magnético na direção oposta. Este é o efeito que fornece o elemento de memória em uma unidade de disco rígido.
A relação entre a indução magnética H e a magnetização M não é linear em tais materiais. Se um ímã é desmagnetizado (H = M = 0) e a relação entre H e M é plotada para aumento dos níveis de intensidade de campo, M segue a curva de magnetização inicial. Esta curva aumenta rapidamente no início e depois se aproxima de uma assíntota chamada saturação magnética. Se o campo magnético é agora reduzido monotonicamente, M segue uma curva diferente. Em uma intensidade de campo igual a zero, a magnetização é compensada a partir da origem de um montante chamado de remanência. Se a relação entre H e M for traçado para todas as forças de campo magnético aplicado o resultado é um ciclo de histerese chamado de loop principal.
Um olhar mais atento em uma curva de magnetização geralmente revela uma série de pequenos saltos aleatórios na magnetização chamados saltos Barkhausen. Este efeito é devido a defeitos cristalográficos tais como deslocamentos.
Origem física[editar | editar código-fonte]
O fenômeno da histerese em materiais ferromagnéticos é o resultado de dois efeitos: a rotação do vetor magnetização e as mudanças no tamanho ou número de domínios magnéticos. Em geral, a magnetização varia (em direção, mas não magnitude) através de um ímã.
Ímãs maiores são divididos em regiões chamadas de domínios. Em cada domínio, a magnetização não varia, mas entre os domínios temos paredes de domínio relativamente finas em que a direção da magnetização gira na direção de um domínio para outro. Se o campo magnético muda, as paredes se movem, mudando assim o tamanho relativo dos domínios.
Aplicações[editar | editar código-fonte]
Há uma grande variedade de aplicações da histerese em ferromagnetos. Muitos destes fazem uso de sua capacidade de reter memória, por exemplo, cartões de fita magnética, discos rígidos, e de crédito. Nestas aplicações, ímãs de disco rígido como o ferro são desejáveis para a memória não ser facilmente apagada.
Método de medição dos campos[editar | editar código-fonte]
O método descrito pelo ciclo de histerese mede o campo de indução magnética  em função do campo magnético
em função do campo magnético  . Se considermos um anel de material ferromagnético de seção A e raio R constante, envolvido por N espiras pelas quais passa uma corrente contínua I. Nesta situação, os campos são circulares dentro do anel e são desprezíveis fora dele. Deste modo se calcula o valor de
. Se considermos um anel de material ferromagnético de seção A e raio R constante, envolvido por N espiras pelas quais passa uma corrente contínua I. Nesta situação, os campos são circulares dentro do anel e são desprezíveis fora dele. Deste modo se calcula o valor de  a partir da Lei de Ampère:
a partir da Lei de Ampère:
 em função do campo magnético
em função do campo magnético  . Se considermos um anel de material ferromagnético de seção A e raio R constante, envolvido por N espiras pelas quais passa uma corrente contínua I. Nesta situação, os campos são circulares dentro do anel e são desprezíveis fora dele. Deste modo se calcula o valor de
. Se considermos um anel de material ferromagnético de seção A e raio R constante, envolvido por N espiras pelas quais passa uma corrente contínua I. Nesta situação, os campos são circulares dentro do anel e são desprezíveis fora dele. Deste modo se calcula o valor de  a partir da Lei de Ampère:
a partir da Lei de Ampère:e, como o anel tem simetria circular, a integral resulta:
Levando em conta a permeabilidade magnética relativa do material  , é possível calcular o campo de indução magnética:
, é possível calcular o campo de indução magnética:
 , é possível calcular o campo de indução magnética:
, é possível calcular o campo de indução magnética:Este sistema é usado na prática para medir os dois campos ao variar a intensidade da corrente:
Por meio desse procedimento é possível obter experimentalmente a curva de magnetização, ou a variação do campo magnético em função do vetor de indução magnética e, portanto, o ciclo de histerese.
Temperatura de Curie[editar | editar código-fonte]
Marie Curie foi a primeira a descobrir que existe uma temperatura crítica para cada material ferromagnético acima da qual o material se comporta como paramagnético. Quando a temperatura aumenta, o movimento térmico compete com a tendência ferromagnética para os dipolos se alinharem. Quando a temperatura sobe além de certo ponto, chamado de temperatura Curie, há uma transição de fase de segunda ordem e o sistema não pode mais manter uma magnetização espontânea, embora ainda responda paramagneticalmente a um campo externo. Abaixo dessa temperatura, há uma quebra espontânea de simetria e forma-se domínios aleatórios (na ausência de um campo externo). A Susceptibilidade magnética segue a lei de Curie-Weiss:
onde C é uma constante característica do material,  sua densidade e
sua densidade e  a temperatura de Curie em kelvin.
a temperatura de Curie em kelvin.
 sua densidade e
sua densidade e  a temperatura de Curie em kelvin.
a temperatura de Curie em kelvin.Modelos teóricos[editar | editar código-fonte]
O ferromagnetismo representa um dos principais problemas em aberto da física do estado sólido. Existem dois modelos teóricos que o descrevam: o modelo de Ising e o modelo de Weiss, o qual será tratado a seguir, ambos sendo baseados na hamiltoniana de Werner Karl Heisenberg, mas que utilizam grandes aproximações.
Hamiltoniana de Heisenberg[editar | editar código-fonte]
A hamiltoniana para um par de elétrons pertencentes a átomos vizinhos é:
onde  e
e  são as hamiltonianas apenas dos elétrons, e
são as hamiltonianas apenas dos elétrons, e  é a interação entre os dois.
é a interação entre os dois.
 e
e  são as hamiltonianas apenas dos elétrons, e
são as hamiltonianas apenas dos elétrons, e  é a interação entre os dois.
é a interação entre os dois.Pelo princípio de exclusão de Pauli, a função de onda total deve ser antissimétrica. Assim, tem-se duas possibilidades:
ou
Onde os subscritos “A” ou “S” indicam uma função antissimétrica/simétrica.
As funções de onda de spin para um par de elétrons são:
As funções de onda “espaciais” são:
Efetuando um cálculo perturbativo sobre tais funções de onda obtêm-se:
Onde J é conhecida como integral de troca, que está relacionada com a Interação de Troca, interação responsável pela tendência dos momentos magnéticos do material a permanecerem paralelos entre si. A hamiltoniana separa, então, os estados com spins diferentes, e por este motivo, Heisenberg encontrou um operador que distinguisse os estados com spin diferente e que então pudesse descrever a interação precedente. Tal operador é:
Logo, a Hamiltoniana de Heisenberg é:
Modelo de Weiss[editar | editar código-fonte]
O modelo de Weiss propõe a generalização da hamiltoniana de Heisenberg para um sistema com mais elétrons, utilizando uma aproximação de campo médio: um elétron sofre uma interação devida à média do campo gerado pelos outros elétrons.
A Hamiltoniana do sistema torna-se então:
Substituindo o momento magnético:
E o vetor magnetização:
Tem-se:
Logo:
Percebe-se uma analogia com o paramagnetismo de Langevin, no qual se faz o mesmo tipo de estudo, substituindo-se o campo magnético por um campo magnético eficaz, dado por:
.
Existe, assim, uma temperatura crítica de Curie:
Abaixo da qual se manifestam os efeitos do ferromagnetismo. As quantidades “s” e “k” são os autovalores do spin e a constante de Boltzmann repectivamente, enquanto  é dado por:
é dado por:
 é dado por:
é dado por:Materiais ferromagnéticos[editar | editar código-fonte]
A seguir, temos uma tabela com alguns materiais ferromagnéticos e suas respectivas temperaturas de Curie.
| Material | Temp. Curie (K) |
|---|---|
| Fe | 1043 |
| Co | 1388 |
| Ni | 627 |
| Gd | 292 |
| Dy | 88 |
| MnAs | 318 |
| MnBi | 630 |
| MnSb | 587 |
| CrO2 | 386 |
| MnOFe2O3 | 573 |
| FeOFe2O3 | 858 |
| NiOFe23 | 858 |
| CuOFe2O3 | 728 |
| MgOFe23 | 713 |
| EuO | 69 |
| Y3Fe5O12 | 560 |
Ferromagnetismo é uma propriedade não apenas da composição química de um material, mas de sua estrutura cristalina e organização microscópica. Existem ligas de metal ferromagnético cujos constituintes não são próprios ferromagnéticos, chamado ligas de Heusler, em homenagem a Fritz Heusler. Por outro lado existem ligas não-magnéticos, como os tipos de aço inoxidável, composto quase exclusivamente de metais ferromagnéticos.
Também se pode fazer ligas metálicas amorfas (não cristalinas) ferromagnéticas por resfriamento muito rápido de uma liga líquida. Estes têm a vantagem de que suas propriedades são quase isotrópicas (não alinhadas ao longo de um eixo do cristal), o que resulta em baixa coercividade, perda de baixa histerese, permeabilidade alta e alta resistividade elétrica. Um material desse tipo é normalmente uma transição liga metal-metalóide, feita a partir de cerca de 80% de metal de transição (normalmente Fe, Co, ou Ni) e um componente de metalóide (B, C, Si, P, ou Al) que reduz o ponto de fusão.
Uma classe relativamente nova de materiais ferromagnéticos excepcionalmente fortes são os ímãs de terras raras. Eles contêm elementos lantanídeos, que são conhecidos por sua capacidade de transportar grandes momentos magnéticos no bem localizado oribital f.
Estadologia Graceli – 4. E princípio entrópico tempo / instabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
![{\displaystyle \left[-{\frac {\hbar ^{2}\nabla ^{2}}{2m}}+V\left(\mathbf {r} ,t\right)\right]\Psi \left(\mathbf {r} ,t\right)=i\hbar {\frac {\partial \Psi \left(\mathbf {r} ,t\right)}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38c283545c0b17f94ae6d445adf312c43536ac5a)

 = entropia reversível
= entropia reversível
 ,
,

 = entropia reversível
= entropia reversível
![{\displaystyle L=\sum _{i=1}^{N}\left[{\frac {1}{2}}m{\dot {x}}^{2}-{\frac {\kappa }{2}}(x_{i}-x_{i+1})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f439a0c94d19464a22cf3261a0e7ceb3298a93c) .
.

 = entropia reversível
= entropia reversível
![{\displaystyle \left[\square +\left({\frac {mc}{\hbar }}\right)^{2}\right]\psi =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9e6b0f901443db31735de1ad80bb7e6fcfcc10)

 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível
![{\displaystyle \left[-{\frac {\hbar ^{2}\nabla ^{2}}{2m}}+V\left(\mathbf {r} ,t\right)\right]\Psi \left(\mathbf {r} ,t\right)=i\hbar {\frac {\partial \Psi \left(\mathbf {r} ,t\right)}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38c283545c0b17f94ae6d445adf312c43536ac5a)
![{\displaystyle \left[-{\frac {\hbar ^{2}\nabla ^{2}}{2m}}+V\left(\mathbf {r} \right)\right]\psi \left(\mathbf {r} \right)=E\psi \left(\mathbf {r} \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a4d448140c182011893cffc80b2d56c290a3a53)
 ,
,
 ,
, ,
, ,
, .
. ,
,
 .
.![{\displaystyle \{A,B\}\to {\frac {i}{\hbar }}[{\hat {A}},{\hat {B}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c169db417903d276a6989dfd5b4088ae87154419) ,
,![{\displaystyle [{\hat {p}}^{i},{\hat {q}}^{j}]=-i\hbar \delta ^{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1753347a289a5703f38397555bd4795c63a22caa) .
.
 ,
,![{\displaystyle L=\sum _{i=1}^{N}\left[{\frac {1}{2}}m{\dot {x}}^{2}-{\frac {\kappa }{2}}(x_{i}-x_{i+1})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f439a0c94d19464a22cf3261a0e7ceb3298a93c) .
.![{\displaystyle L=\int dx{\frac {1}{2}}\left[\mu {\dot {\phi (t,x)}}^{2}-\nu \left({\frac {d\phi (t,x)}{dx}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6444a26627a97fdf1bba5249dbb6d9f341e6a36c) ,
, .
. ,
, .
.
![{\displaystyle \left[\square +\left({\frac {mc}{\hbar }}\right)^{2}\right]\psi =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9e6b0f901443db31735de1ad80bb7e6fcfcc10)








 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível
 .
.
 = entropia reversível
= entropia reversível



![E(x,t)=E_{{\text{máx}}}\,\sin {\Bigg [}{\frac {2\,\pi }{\lambda }}\,(x-c\,t)+\varphi {\Bigg ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e4376e56e10d2cc7900bb94081fd07996e01fbb)


 .
. .
. Ver artigo principal: Radiação de corpo negro
Ver artigo principal: Radiação de corpo negro


 = entropia reversível
= entropia reversível



 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível

 (P)
(P)
 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível













 (P)
(P)




 (T)
(T)








 ou
ou 


tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Teoria quântica de campos e unificações no sistema decadimensional e categorial Graceli
terça-feira, 22 de janeiro de 2019
![{\displaystyle \left[-{\frac {\hbar ^{2}\nabla ^{2}}{2m}}+V\left(\mathbf {r} ,t\right)\right]\Psi \left(\mathbf {r} ,t\right)=i\hbar {\frac {\partial \Psi \left(\mathbf {r} ,t\right)}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38c283545c0b17f94ae6d445adf312c43536ac5a)
x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
 ,
,x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
![{\displaystyle L=\sum _{i=1}^{N}\left[{\frac {1}{2}}m{\dot {x}}^{2}-{\frac {\kappa }{2}}(x_{i}-x_{i+1})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f439a0c94d19464a22cf3261a0e7ceb3298a93c) .
.x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
![{\displaystyle \left[\square +\left({\frac {mc}{\hbar }}\right)^{2}\right]\psi =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9e6b0f901443db31735de1ad80bb7e6fcfcc10)
x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Advento da teoria clássica dos campos[editar | editar código-fonte]
Pode-se considerar que a noção de campo surgiu inicialmente como uma construção matemática na descrição da gravitação newtoniana. No século XIX, tal formalismo logo foi estendido tanto para fenômenos elétricos quanto magnéticos por físicos como Ampère, Ohm e Faraday.
Devido aos trabalhos de Maxwell, o conceito de campo passa a ocupar o papel de maior importância na descrição fenomenológica da realidade. Maxwell mostrou, através de um conjunto de equações que recebem seu nome, que os fenômenos magnéticos e elétricos estão intrinsecamente associados e que devem ser descritos por uma única entidade: o campo eletromagnético [4].
Conceitualmente, Maxwell mostrou a relação entre campos elétricos e magnéticos, bem como o reconhecimento de que a luz (óptica) é uma manifestação particular deste campo eletromagnético. Dentro dessa perspectiva histórica, a unificação dos fenômenos eletromagnéticos realizado por Maxwell foi a segunda grande unificação, a primeira sendo a unificação da dinâmica celeste e terrestre realizada por Isaac Newton ainda no século XVII [5].
Mecânica, Eletromagnetismo e Relatividade[editar | editar código-fonte]
O eletromagnetismo foi a "raison d’être" do surgimento da relatividade. Com a inadequação das transformações de Galileu quando aplicadas à equação de onda tridimensional, surgiu um dilema: ou se preservava a mecânica clássica e abandonava-se o nascente eletromagnetismo, ou se preservava este e abandonava-se quase três séculos de previsões solidamente confirmadas pela experimentação.
O caminho foi achado, surpreendemente, numa espécie de conciliação entre as duas alternativas.
Inicialmente, Woldemar Voigt derivou em 1887 um conjunto de relações, baseado apenas na equação de onda ordinária, devida a Jean D'Alembert. Essas relações eram transformações espaciais e temporais que deixavam invariante a forma desta equação.
Estas relações são as que se conhecem como transformações de Lorentz-Fitzgerald, cientistas que redescobriram estas transformações mais tarde. Em particular, Lorentz o fez num contexto diferente, na tentativa de se reconciliar as teorias do éter com os resultados de experiências físicas, tais como a de Michelson-Morley. Einstein então entra em cena, com seu trabalho seminal de 1905, "Sobre a Eletrodinâmica dos Corpos em Movimento", onde introduz a relatividade, interpretando corretamente as transformações de Lorentz-Fitzgerald como alterações do espaço e do tempo em função da velocidade relativa entre os referenciais.
Termodinâmica e mecânica quântica[editar | editar código-fonte]A mecânica quântica surgiu da incapacidade conjunta da termodinâmica e do eletromagnetismo clássicos de prever a correta distribuição de energias em função da frequência no problema da radiação de corpo negro.
A tentativa de derivação feita por Lord Rayleigh e por James Jeans postulava que cada onda eletromagnética estava em equilíbrio com as paredes do forno. Isso se traduz num teorema que mantém sua validade mesmo na mecânica quântica:
Numa cavidade fechada em equilíbrio térmico com o campo eletromagnético confinado, o campo é equivalente a um conjunto enumeravelmente infinito de osciladores harmônicos, e a sua energia é igual à soma das energias desses osciladores. Cada frequência corresponde aos osciladores tomados dois a dois.
Max Planck obteve a forma correta da distribuição porque postulou a quantização da energia dos osciladores harmônicos que comporiam as paredes da cavidade que confina a radiação. Essa hipótese teve por efeito introduzir um limite máximo de freqüência acima do qual há um corte (cutoff) nas contribuições dos entes (ondas eletromagnéticas) que estão em equilíbrio.
Einstein, para explicar o efeito fotoelétrico, ampliou o conceito da quantização para a energia radiante, postulando a existência do fóton (o que "implicitamente" quer dizer que as equações de Maxwell não tem validade ilimitada, porque a existência do fóton implica não-linearidades).
A antiga teoria quântica cedeu lugar à mecânica quântica moderna quando Schrödinger desenvolveu a famosa equação que leva o seu nome. Entretanto, a primeira versão que ele desenvolveu foi a equação que hoje é conhecida como equação de Klein-Gordon, que é uma equação relativista, mas que não descrevia bem o átomo de hidrogênio, por razões que só mais tarde puderam ser entendidas. Assim, ele abandonou a primeira tentativa, chegando à sua equação (equação de Schrödinger):
![{\displaystyle \left[-{\frac {\hbar ^{2}\nabla ^{2}}{2m}}+V\left(\mathbf {r} ,t\right)\right]\Psi \left(\mathbf {r} ,t\right)=i\hbar {\frac {\partial \Psi \left(\mathbf {r} ,t\right)}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38c283545c0b17f94ae6d445adf312c43536ac5a)
A equação de Schrödinger acima colocada é a equação "dependente do tempo", pois o tempo aparece explicitamente. Neste caso, as soluções  são funções das coordenadas espaciais e do tempo.
são funções das coordenadas espaciais e do tempo.
 são funções das coordenadas espaciais e do tempo.
são funções das coordenadas espaciais e do tempo.Quando o potencial  não depende do tempo, ou seja, quando o campo de força ao qual a partícula está submetida é conservativo, é possível separar as variáveis
não depende do tempo, ou seja, quando o campo de força ao qual a partícula está submetida é conservativo, é possível separar as variáveis  e
e  .
.
 não depende do tempo, ou seja, quando o campo de força ao qual a partícula está submetida é conservativo, é possível separar as variáveis
não depende do tempo, ou seja, quando o campo de força ao qual a partícula está submetida é conservativo, é possível separar as variáveis  e
e  .
.A equação que a parte espacial da função de onda  obedece é:
obedece é:
 obedece é:
obedece é:![{\displaystyle \left[-{\frac {\hbar ^{2}\nabla ^{2}}{2m}}+V\left(\mathbf {r} \right)\right]\psi \left(\mathbf {r} \right)=E\psi \left(\mathbf {r} \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a4d448140c182011893cffc80b2d56c290a3a53)
conhecida como equação de Schrödinger "independente do tempo". Esta é uma equação de autovalores, ou seja, através dela se obtêm simultaneamente autofunções (no caso as funções de onda  ) e autovalores (no caso, o conjunto das energias estacionárias
) e autovalores (no caso, o conjunto das energias estacionárias  ).
).
 ) e autovalores (no caso, o conjunto das energias estacionárias
) e autovalores (no caso, o conjunto das energias estacionárias  ).
).Formulação matemática[editar | editar código-fonte]
Mecânica clássica e mecânica quântica[editar | editar código-fonte]
A dinâmica de uma partícula pontual de massa  em um regime não-relativístico, ou seja, em velocidades muito menores que a velocidade da luz, pode ser determinada através da função lagrangiana [6][7]
em um regime não-relativístico, ou seja, em velocidades muito menores que a velocidade da luz, pode ser determinada através da função lagrangiana [6][7]
 em um regime não-relativístico, ou seja, em velocidades muito menores que a velocidade da luz, pode ser determinada através da função lagrangiana [6][7]
em um regime não-relativístico, ou seja, em velocidades muito menores que a velocidade da luz, pode ser determinada através da função lagrangiana [6][7]  ,
,em que  (que são respectivamente coordenadas generalizadas para a posição e a velocidade da partícula) determinam o espaço de fase do sistema e
(que são respectivamente coordenadas generalizadas para a posição e a velocidade da partícula) determinam o espaço de fase do sistema e  é o potencial em que a partícula se move. Minimizando o funcional ação
é o potencial em que a partícula se move. Minimizando o funcional ação
 (que são respectivamente coordenadas generalizadas para a posição e a velocidade da partícula) determinam o espaço de fase do sistema e
(que são respectivamente coordenadas generalizadas para a posição e a velocidade da partícula) determinam o espaço de fase do sistema e  é o potencial em que a partícula se move. Minimizando o funcional ação
é o potencial em que a partícula se move. Minimizando o funcional ação
encontra-se a equação de movimento para esse sistema,
 ,
,que é a equação de Newton, desde que  .
.
 .
. Existe outra formulação equivalente da mecânica clássica, conhecida como formulação hamiltoniana e que pode ser diretamente relacionada a formulação lagrangiana acima. Para se fazer contato entre as duas formulações, define-se o momento
 ,
,de maneira que a função hamiltoniana é dada por
 ,
,que para a escolha da lagrangiana acima, tem-se
 .
.Assim como no caso da função lagrangiana, a hamiltoniana descreve toda a dinâmica de um sistema clássico, portanto, considerando uma variação de  tem-se um par de equações diferenciais de primeira ordem conhecidas como equações de Hamilton
tem-se um par de equações diferenciais de primeira ordem conhecidas como equações de Hamilton
 tem-se um par de equações diferenciais de primeira ordem conhecidas como equações de Hamilton
tem-se um par de equações diferenciais de primeira ordem conhecidas como equações de Hamilton  ,
,e que equivale a equação de Newton, que é de segunda ordem. No formalismo hamiltoniano, usando a regra da cadeia, pode-se escrever qualquer variação temporal de uma função  , em termos das equações de Hamilton acima, de modo que,
, em termos das equações de Hamilton acima, de modo que,
 , em termos das equações de Hamilton acima, de modo que,
, em termos das equações de Hamilton acima, de modo que,
onde o parêntese de Poisson é definido como
 .
.Existem diversas maneiras de realizar a quantização de um sistema clássico, tais como quantização por integrais funcionais e quantização canônica. Esse último método em particular, consiste na substituição do parêntese de Poisson por comutadores[8]
![{\displaystyle \{A,B\}\to {\frac {i}{\hbar }}[{\hat {A}},{\hat {B}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c169db417903d276a6989dfd5b4088ae87154419) ,
,onde  , são operadores num espaço de Hilbert. Com essas substituições, o parêntese de Poisson entre duas coordenadas generalizadas torna-se
, são operadores num espaço de Hilbert. Com essas substituições, o parêntese de Poisson entre duas coordenadas generalizadas torna-se
 , são operadores num espaço de Hilbert. Com essas substituições, o parêntese de Poisson entre duas coordenadas generalizadas torna-se
, são operadores num espaço de Hilbert. Com essas substituições, o parêntese de Poisson entre duas coordenadas generalizadas torna-se![{\displaystyle [{\hat {p}}^{i},{\hat {q}}^{j}]=-i\hbar \delta ^{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1753347a289a5703f38397555bd4795c63a22caa) .
.Um aspecto importante a ser observado é que os operadores  e
e  podem ser representados como os operadores diferencias
podem ser representados como os operadores diferencias
 e
e  podem ser representados como os operadores diferencias
podem ser representados como os operadores diferencias
de maneira que a função hamiltoniana, torna-se um operador no espaço de Hilbert, chamado operador hamiltoniano que atua em uma função 

 ,
,que é a equação de Schrödinger.
Teoria Clássica de Campos[editar | editar código-fonte]
A formulação lagrangiana e a hamiltoniana da mecânica clássica são refinamentos da mecânica newtoniana e permite o tratamento de sistemas com um número finito de graus de liberdade. Considerando um sistema mecânico unidimensional com  graus de liberdade, que consiste de
graus de liberdade, que consiste de  partículas pontuais de massa
partículas pontuais de massa  , separadas por uma distância
, separadas por uma distância  e conectadas entre si por uma mola de constante elástica
e conectadas entre si por uma mola de constante elástica  . A lagrangiana para esse sistema é:
. A lagrangiana para esse sistema é:
 graus de liberdade, que consiste de
graus de liberdade, que consiste de  partículas pontuais de massa
partículas pontuais de massa  , separadas por uma distância
, separadas por uma distância  e conectadas entre si por uma mola de constante elástica
e conectadas entre si por uma mola de constante elástica  . A lagrangiana para esse sistema é:
. A lagrangiana para esse sistema é:![{\displaystyle L=\sum _{i=1}^{N}\left[{\frac {1}{2}}m{\dot {x}}^{2}-{\frac {\kappa }{2}}(x_{i}-x_{i+1})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f439a0c94d19464a22cf3261a0e7ceb3298a93c) .
.Esse sistema pode ser estendido facilmente para o limite em que  e
e  . No entanto, se o comprimento total do sistema estiver fixo, tem-se o limite contínuo
. No entanto, se o comprimento total do sistema estiver fixo, tem-se o limite contínuo  , de modo que a lagrangiana terá a forma
, de modo que a lagrangiana terá a forma
 e
e  . No entanto, se o comprimento total do sistema estiver fixo, tem-se o limite contínuo
. No entanto, se o comprimento total do sistema estiver fixo, tem-se o limite contínuo  , de modo que a lagrangiana terá a forma
, de modo que a lagrangiana terá a forma![{\displaystyle L=\int dx{\frac {1}{2}}\left[\mu {\dot {\phi (t,x)}}^{2}-\nu \left({\frac {d\phi (t,x)}{dx}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6444a26627a97fdf1bba5249dbb6d9f341e6a36c) ,
,onde  representa o deslocamento da partícula relativa a posição
representa o deslocamento da partícula relativa a posição  no instante de tempo
no instante de tempo  . Também, define-se as quantidades
. Também, define-se as quantidades 
 .
.
 representa o deslocamento da partícula relativa a posição
representa o deslocamento da partícula relativa a posição  no instante de tempo
no instante de tempo  . Também, define-se as quantidades
. Também, define-se as quantidades 
 .
.Generalizando essa discussão prévia para um sistema relativístico, tem-se uma lagrangiana que será uma função do campo  , em que
, em que  e das derivadas
e das derivadas  , dessa maneira, o funcional ação pode ser escrito como
, dessa maneira, o funcional ação pode ser escrito como
 , em que
, em que  e das derivadas
e das derivadas  , dessa maneira, o funcional ação pode ser escrito como
, dessa maneira, o funcional ação pode ser escrito como .
.Finalmente, a lagrangiana pode ser escrita como
 ,
,onde  , é conhecida como densidade lagrangiana [9]. A equação de Euler-Lagrange é:
, é conhecida como densidade lagrangiana [9]. A equação de Euler-Lagrange é:
 , é conhecida como densidade lagrangiana [9]. A equação de Euler-Lagrange é:
, é conhecida como densidade lagrangiana [9]. A equação de Euler-Lagrange é: .
.Primeiras unificações. Equações relativísticas[editar | editar código-fonte]
| Esta seção não cita fontes confiáveis e independentes, o que compromete sua credibilidade (desde fevereiro de 2018). Por favor, adicione referências e insira-as corretamente no texto ou no rodapé. Conteúdo sem fontes poderá ser removido. —Encontre fontes: Google (notícias, livros e acadêmico) |
Equação de Klein-Gordon[editar | editar código-fonte]
Como foi dito acima, quando Schrödinger primeiro procurou uma equação que regesse os sistemas quânticos, pautou sua busca admitindo uma aproximação relativista, encontrando a depois redescoberta equação de Klein-Gordon:
![{\displaystyle \left[\square +\left({\frac {mc}{\hbar }}\right)^{2}\right]\psi =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9e6b0f901443db31735de1ad80bb7e6fcfcc10)
onde

A equação de Klein-Gordon, às vezes chamada de equação de Klein-Fock-Gordon (ou ainda Klein-Gordon-Fock) pode ser deduzida de algumas maneiras diferentes.
Usando-se a definição relativística de energia

chega-se à equação:

Essa expressão, por conter operadores diferenciais sob o radical, além de apresentar dificuldades computacionais, também apresenta dificuldades conceituais, já que se torna uma teoria não-local (pelo fato de a raiz poder ser expressa como uma série infinita). Por ser uma equação de segunda ordem não permite que fique bem definida a questão da normalização da função de onda.
Fock deduziu-a através da generalização da equação de Schrödinger para campos magnéticos (onde as forças dependem da velocidade). Fock e Klein usaram ambos o método de Kaluza-Klein para deduzi-la. O motivo, só mais tarde entendido, da inadequação desta equação ao átomo de hidrogênio é que ela se aplica bem somente a partículas sem carga e de spin nulo.
Equação de Dirac[editar | editar código-fonte]
Em 1928 Paul Dirac obteve uma equação relativística baseada em dois princípios básicos
- A equação deveria ser linear na derivada temporal;
- A equação deveria ser relativisticamente covariante.
A equação obtida por ele tinha a seguinte forma:

onde  ,
,  ,
,  e
e  não são números reais ou complexos, mas sim matrizes quadradas com N² componentes. Semelhantemente, as funções
não são números reais ou complexos, mas sim matrizes quadradas com N² componentes. Semelhantemente, as funções  são na verdade matrizes coluna da forma
são na verdade matrizes coluna da forma
 ,
,  ,
,  e
e  não são números reais ou complexos, mas sim matrizes quadradas com N² componentes. Semelhantemente, as funções
não são números reais ou complexos, mas sim matrizes quadradas com N² componentes. Semelhantemente, as funções  são na verdade matrizes coluna da forma
são na verdade matrizes coluna da forma
A equação de Dirac, diferentemente da equação de Klein-Gordon, é uma equação que dá bons resultados para partículas de spin ½. Aliás, um dos sucessos é que esta equação incorpora o spin de forma natural, o que não ocorre com a equação de Schrondinger, onde o spin é admitido posteriormente como uma hipótese ad hoc. Não obstante, isso levou certos autores a afirmarem que o spin é um grau de liberdade relativístico, o que é contestado. Outro sucesso da equação de Dirac foi prever a existencia do pósitron, já que a equação previa valores negativos de energia, o que foi inicialmente interpretado, à luz da [[teoria dos buracos], como indicação de elétrons com energias negativas. Essa teoria afirmava que os pósitrons seriam vacâncias produzidas pela promoção desses elétrons para estados com energias positivas. O vácuo é então visto como um mar de elétrons onde eles estariam compactamente colocados. Hoje, entretanto, essa teoria cedeu lugar à questão de criação e aniquilação de partículas num contexto mais geral da quantização canônica dos campos.
Desenvolvimento da teoria quântica dos campos[editar | editar código-fonte]
A origem da teoria quântica dos campos é marcada pelos estudos de Max Born e Pascual Jordan em 1925 sobre o problema da computação da potência irradiada de um átomo em uma transição energética.
Em 1926, Born, Jordan e Werner Heisenberg formularam a teoria quântica do campo eletromagnético desprezando tanto a polarização como a presença de fontes, levando ao que se chama hoje de uma teoria do campo livre. Para tanto, usaram o procedimento da quantização canônica.
Três razões principais motivaram o desenvolvimento da teoria quântica dos campos:
- A necessidade da uma teoria que lidasse com a variação do número de partículas;
- A necessidade de conciliação entre as duas teorias: mecânica quântica e a relatividade;
- A necessidade de lidar com estatísticas de sistemas multipartículas.
Quantização canônica dos campos[editar | editar código-fonte]
Um campo, no esquema conceitual da teoria dos campos, é uma entidade com infinitos graus de liberdade.
O estado de mais baixa energia, chamado de vácuo, corresponde à ausência de partículas.
Estas, entretanto, podem ser criadas ou destruídas através de dois operadores:
: operador criação
: operador aniquilação
que agem sobre a função de onda do campo, respectivamente simbolizando a criação e a aniquilação de partículas dotadas de momento  , possibilidade exigida pela relatividade.
, possibilidade exigida pela relatividade.
 , possibilidade exigida pela relatividade.
, possibilidade exigida pela relatividade.Os operadores, agindo sobre os estados de um tipo específico de espaço de Hilbert, chamado espaço de Fock, criam e destroem as partículas. Entretanto, uma restrição é:

o que quer dizer que não pode haver aniquilação sobre o estado básico, já que nesse caso não há partículas a serem aniquiladas.
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Pos
Radiação eletromagnética + entropia quântica no sistema decadimensional e categorial Graceli
quinta-feira, 31 de janeiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
 .
.x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
A radiação eletromagnética é uma oscilação em fase dos campos elétricos e magnéticos, que, autossustentando-se, encontram-se desacoplados das cargas elétricas que lhe deram origem. As oscilações dos campos magnéticos e elétricos são perpendiculares entre si e podem ser entendidas como a propagação de uma onda transversal, cujas oscilações são perpendiculares à direção do movimento da onda (como as ondas da superfície de uma lâmina de água), que pode se deslocar através do vácuo. Dentro do ponto de vista da Mecânica Quântica, podem ser entendidas, ainda, como o deslocamento de pequenas partículas, os fótons.
O espectro visível, ou simplesmente luz visível, é apenas uma pequena parte de todo o espectro da radiação eletromagnética possível, que vai desde as ondas de rádio aos raios gama. A existência de ondas eletromagnéticas foi prevista por James Clerk Maxwell e confirmada experimentalmente por Heinrich Hertz. A radiação eletromagnética encontra aplicações como a radiotransmissão, seu emprego no aquecimento de alimentos (fornos de micro-ondas), em lasers para corte de materiais ou mesmo na simples lâmpada incandescente.
A radiação eletromagnética pode ser classificada de acordo com a frequência da onda, em ordem crescente, nas seguintes faixas: ondas de rádio, micro-ondas, radiação terahertz, radiação infravermelha, luz visível, radiação ultravioleta, raios X e radiação gama.
Ondas eletromagnéticas

Representação esquemática de uma onda eletromagnética linearmente polarizada produzida por um dipolo elétrico oscilante (à esquerda). A onda se propaga ao longo do eixo horizontal com comprimento de onda λ (ao centro). O campo elétrico, o campo magnético e o vetor de onda são representados, respectivamente, em azul, vermelho e preto (à direita).
As ondas eletromagnéticas primeiramente foram previstas teoricamente por James Clerk Maxwell e depois confirmadas experimentalmente por Heinrich Hertz. Maxwell notou as ondas a partir de equações de electricidade e magnetismo, revelando sua natureza e sua simetria. Faraday mostrou que um campo magnético variável no tempo gera um campo eléctrico. Maxwell mostrou que um campo eléctrico variável com o tempo gera um campo magnético, com isso há uma autossustentação entre os campos eléctrico e magnético. Em seu trabalho de 1862, Maxwell escreveu:
"A velocidade das ondas transversais em nosso meio hipotético, calculada a partir dos experimentos electromagnéticos dos Srs. Kohrausch e Weber, concorda tão exactamente com a velocidade da luz, calculada pelos experimentos óticos do Sr. Fizeau, que é difícil evitar a inferência de que a luz consiste nas ondulações transversais do mesmo meio que é a causa dos fenômenos eléctricos e magnéticos."[carece de fontes]
Ondas harmônicas[editar | editar código-fonte]
Uma onda harmônica é uma onda com a forma de uma função senoidal, como na figura , no caso de uma onda que se desloca no sentido positivo do eixo dos  .
.
 .
.A distância  entre dois pontos consecutivos onde o campo e a sua derivada têm o mesmo valor, é designada por [comprimento de onda] (por exemplo, a distância entre dois máximos ou mínimos consecutivos). O valor máximo do módulo do campo,
entre dois pontos consecutivos onde o campo e a sua derivada têm o mesmo valor, é designada por [comprimento de onda] (por exemplo, a distância entre dois máximos ou mínimos consecutivos). O valor máximo do módulo do campo,  , é a sua {amplitude}.
, é a sua {amplitude}.
 entre dois pontos consecutivos onde o campo e a sua derivada têm o mesmo valor, é designada por [comprimento de onda] (por exemplo, a distância entre dois máximos ou mínimos consecutivos). O valor máximo do módulo do campo,
entre dois pontos consecutivos onde o campo e a sua derivada têm o mesmo valor, é designada por [comprimento de onda] (por exemplo, a distância entre dois máximos ou mínimos consecutivos). O valor máximo do módulo do campo,  , é a sua {amplitude}.
, é a sua {amplitude}.O tempo que a onda demora a percorrer um comprimento de onda designa-se por {período},  .
.
 .
.O inverso do período é a frequência  , que indica o número de comprimentos de onda que passam por um ponto, por unidade de tempo. No sistema SI a unidade da frequência é o hertz, representado pelo símbolo Hz, equivalente a
, que indica o número de comprimentos de onda que passam por um ponto, por unidade de tempo. No sistema SI a unidade da frequência é o hertz, representado pelo símbolo Hz, equivalente a  .
.
 , que indica o número de comprimentos de onda que passam por um ponto, por unidade de tempo. No sistema SI a unidade da frequência é o hertz, representado pelo símbolo Hz, equivalente a
, que indica o número de comprimentos de onda que passam por um ponto, por unidade de tempo. No sistema SI a unidade da frequência é o hertz, representado pelo símbolo Hz, equivalente a  .
.No caso de uma onda eletromagnética no vácuo, a velocidade de propagação é  que deverá verificar a relação:
que deverá verificar a relação:
 que deverá verificar a relação:
que deverá verificar a relação:
A equação da função representada na figura acima é:

onde a constante  é a{fase inicial}. Essa função representa a forma da onda num instante inicial, que podemos admitir
é a{fase inicial}. Essa função representa a forma da onda num instante inicial, que podemos admitir  .
.
 é a{fase inicial}. Essa função representa a forma da onda num instante inicial, que podemos admitir
é a{fase inicial}. Essa função representa a forma da onda num instante inicial, que podemos admitir  .
.Para obter a função de onda num instante diferente, teremos que substituir  por
por  , já que a onda se propaga no sentido positivo do eixo dos
, já que a onda se propaga no sentido positivo do eixo dos  , com velocidade
, com velocidade  .
.
 por
por  , já que a onda se propaga no sentido positivo do eixo dos
, já que a onda se propaga no sentido positivo do eixo dos  , com velocidade
, com velocidade  .
.![E(x,t)=E_{{\text{máx}}}\,\sin {\Bigg [}{\frac {2\,\pi }{\lambda }}\,(x-c\,t)+\varphi {\Bigg ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e4376e56e10d2cc7900bb94081fd07996e01fbb)
usando a relação entre a velocidade e o período, podemos escrever:

Se substituirmos  , obteremos a equação que descreve o campo elétrico na origem, em função do tempo:
, obteremos a equação que descreve o campo elétrico na origem, em função do tempo:
 , obteremos a equação que descreve o campo elétrico na origem, em função do tempo:
, obteremos a equação que descreve o campo elétrico na origem, em função do tempo:
assim, o campo na origem é uma função sinusoidal com período  e amplitude
e amplitude  . O campo em outros pontos tem exatamente a mesma forma sinusoidal, mas com diferentes valores da fase.[1]
. O campo em outros pontos tem exatamente a mesma forma sinusoidal, mas com diferentes valores da fase.[1]
 e amplitude
e amplitude  . O campo em outros pontos tem exatamente a mesma forma sinusoidal, mas com diferentes valores da fase.[1]
. O campo em outros pontos tem exatamente a mesma forma sinusoidal, mas com diferentes valores da fase.[1]Propriedades[editar | editar código-fonte]
Os campos eléctrico e magnético obedecem aos princípios da superposição de ondas, de modo que seus vectores se cruzam e criam os fenômenos da refracção e da difração.[carece de fontes] Uma onda eletromagnética pode interagir com a matéria e, em particular, perturbar átomos e moléculas que as absorvem, podendo os mesmos emitir ondas em outra parte do espectro.
Como qualquer fenômeno ondulatório, as ondas eletromagnéticas podem interferir entre si. Sendo a luz uma oscilação, ela não é afetada pela estática eléctrica ou por campos magnéticos de uma outra onda eletromagnética no vácuo. Em um meio não linear, como um cristal, por exemplo, interferências podem acontecer e causar o efeito Faraday, em que a onda pode ser dividida em duas partes com velocidades diferentes.[carece de fontes]
Na refracção, uma onda, transitando de um meio para outro de densidade diferente, tem alteradas sua velocidade e sua direcção (caso esta não seja perpendicular à superfície) ao entrar no novo meio. A relação entre os índices de refracção dos dois meios determina a escala de refração medida pela lei de Snell:
Nesta equação, i é o ângulo de incidência, N1 é o índice de refração do meio 1, r é o ângulo de refração, e N2 é o índice de refração do meio 2.
A luz se dispersa em um espectro visível porque é reflectida por um prisma, devido ao fenômeno da refração. As características das ondas eletromagnéticas demonstram as propriedades de partículas e do onda ao mesmo tempo, e se destacam mais quando a onda é mais prolongada.
Modelo de onda eletromagnética[editar | editar código-fonte]
Um importante aspecto da natureza da luz é a frequência uma onda, sua taxa de oscilação. É medida em hertz, a unidade SIU de frequência, na qual um hertz (1,00 Hz) é igual a uma oscilação por segundo. A luz normalmente tem um espectro de frequências que, somadas, juntos formam a onda resultante. Diferentes frequências formam diferentes ângulos de refração. Uma onda consiste nos sucessivos baixos e altos, e a distância entre dois pontos altos ou baixos é chamado de comprimento de onda. Ondas eletromagnéticas variam de acordo com o tamanho, de ondas de tamanhos de prédios a ondas gama pequenas menores que um núcleo atômico. A frequência é inversamente proporcional ao comprimento da onda, de acordo com a equação:
 .
.Na passagem de um meio material para outro, a velocidade da onda muda, mas a frequência permanece constante. A interferência acontece quando duas ou mais ondas resultam em um novo padrão de onda. Se os campos tiverem as componentes nas mesmas direções, uma onda "coopera" com a outra (interferência construtiva); entretanto, se estiverem em posições opostas, pode haver uma interferência destrutiva.
Modelo de partículas[editar | editar código-fonte]
Um feixe luminoso é composto por pacotes discretos de energia, caracterizados por consistirem em partículas denominadas fotões (português europeu) ou fótons (português brasileiro). A frequência da onda é proporcional à magnitude da energia da partícula. Como os fótons são emitidos e absorvidos por partículas, eles actuam como transportadores de energia. A energia de um fóton é calculada pela equação de Planck-Einstein:
 .
.Nesta equação, E é a energia, h é a constante de Planck, e f é a frequência.
Se um fóton for absorvido por um átomo, ele excita um electrão (português europeu) ou elétron (português brasileiro), elevando-o a um alto nível de energia. Se o nível de energia é suficiente, ele pula para outro nível maior de energia, podendo escapar da atração do núcleo e ser liberado em um processo conhecido como fotoionização. Um elétron que descer ao nível de energia menor emite um fóton de luz igual a diferença de energia. Como os níveis de energia em um átomo são discretos, cada elemento tem suas próprias características de emissão e absorção.[carece de fontes]
Espectro eletromagnético[editar | editar código-fonte]
O espectro eletromagnético é classificado normalmente pelo comprimento da onda, como as ondas de rádio, as micro-ondas, a radiação infravermelha, a luz visível, os raios ultravioleta, os raios X, até a radiação gama.
O comportamento da onda eletromagnética depende do seu comprimento de onda. Ondas com frequências altas possuem comprimento de onda curto e, por outro lado, ondas com frequências baixas possuem comprimento de onda longo . Quando uma onda interage com uma única partícula ou molécula, seu comportamento depende da quantidade de fótons por ela carregada.[carece de fontes] Através da técnica denominada Espectroscopia óptica, é possível obter-se informações sobre uma faixa visível mais larga do que a visão normal. Um espectroscópio comum pode detectar comprimentos de onda de 2 nm a 2500 nm.
Essas informações detalhadas podem informar propriedades físicas dos objetos, gases e até mesmo estrelas. Por exemplo, um átomo de hidrogênio emite ondas em comprimentos de 21,12 cm. A luz propriamente dita corresponde à faixa que é detectada pelo olho humano, entre 400 nm a 700 nm (um nanômetro vale 1,0×10−9 metro). As ondas de rádio são formadas de uma combinação de amplitude, frequência e fase da onda com a banda da frequência.
Interação da radiação com a matéria[editar | editar código-fonte]
Efeitos biológicos[editar | editar código-fonte]
O efeito biológico mais óbvio das ondas eletromagnéticas se dá em nossos olhos: a luz visível impressiona as células do fundo da retina, causando a sensação visual. Porém, existem outros efeitos mais sutis.
Sabe-se que, em determinadas frequências, as ondas eletromagnéticas podem interagir com moléculas presentes em organismos vivos, por ressonância, isto é, as moléculas cujas frequências fundamentais sejam iguais à da onda em questão "captam" essa oscilação, como uma antena de TV. O efeito sobre a molécula depende da intensidade (amplitude) da onda, podendo ir do simples aquecimento à modificação da estrutura molecular.[carece de fontes] O exemplo mais fácil de ser observado no dia a dia é o de um forno de micro-ondas: as micro-ondas do aparelho, capazes de aquecer a água presente nos alimentos, têm exatamente o mesmo efeito sobre um tecido vivo. Os efeitos da exposição de um animal a uma fonte potente de micro-ondas podem ser catastróficos. Por isso se exige o isolamento físico de equipamentos de telecomunicações que trabalham na faixa de micro-ondas, como as estações rádio-base de telefonia celular.
Assim como as micro-ondas afetam a água, ondas em outra frequência de ressonância podem afetar uma infinidade de outras moléculas. Já foi sugerido que a proximidade a linhas de transmissão teria relações com casos de câncer em crianças, por via de supostas alterações no DNA, provocadas pela prolongada exposição ao campo eletromagnético gerado pelos condutores. Também já se especulou que o uso excessivo do telefone celular teria relação com casos de câncer no cérebro, pelo mesmo motivo. Até hoje, nada disso foi provado.[carece de fontes]
Também já foram feitas experiências para analisar o efeito de campos magnéticos sobre o crescimento de plantas, sem nenhum resultado conclusivo.
Radiação de corpo negro[editar | editar código-fonte]
A radiação de corpo negro, também conhecida por radiação térmica, é a radiação eletromagnética emitida por um corpo em qualquer temperatura[2], constituindo uma forma de transmissão de calor, ou seja, por meio deste tipo de radiação ocorre transferência de energia térmica na forma de ondas eletromagnéticas. Quando a matéria emite e absorve perfeitamente qualquer comprimento de onda e está em equilíbrio termodinâmico, considera-se que é um corpo negro, e sua radiação é chamada de radiação de corpo negro.[3]
A energia cinética de átomos e moléculas varia, converte-se em energia térmica e resulta na radiação eletromagnética térmica. Como as ondas eletromagnéticas também podem se propagar no vácuo, a transferência de calor de um corpo a outro ocorre mesmo se não existir meio material entre os dois, como é o caso da energia emitida pelo Sol e que chega à Terra.
A Lei de Wien relaciona o comprimento de onda em que há máxima emissão de radiação de corpo negro com uma temperatura e determina que o comprimento de onda emitido diminui com o aumento da temperatura. A Lei de Planck para radiação de corpo negro exprime a radiância espectral em função do comprimento de onda e da temperatura do corpo negro e fornece a distribuição dos comprimentos de onda no espectro em função da temperatura. A maior parte da irradiação ocorre em um comprimento de ondaespecífico, chamado de comprimento de onda principal de irradiação, que depende da temperatura do corpo. Quanto maior a temperatura, maior a frequência da radiação e menor o comprimento de onda.
Aplicações tecnológicas[editar | editar código-fonte]
Entre inúmeras aplicações destacam-se o rádio, a televisão, radares, os sistemas de comunicação sem fio (telefonia celular e comunicação wi-fi), os sistemas de comunicação baseados em fibras ópticas e fornos de micro-ondas. Existem equipamentos para a esterilização de lâminas baseados na exposição do instrumento a determinada radiação ultravioleta, produzida artificialmente por uma lâmpada de luz negra.[carece de fontes]
Estadologia Graceli – 4. E princípio entrópico tempo / instabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Número quântico + entropia no sistema decadimensional e categorial Graceli
segunda-feira, 21 de janeiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Os números quânticos descrevem valores de quantidades conservadas na dinâmica de um sistema quântico. No caso dos elétrons, os números quânticos podem ser definidos como "os conjuntos de valores numéricos que dão soluções aceitáveis para a equação de onda de Schrödinger para o átomo de hidrogênio" [1], e são de enorme relevância quando se trata de descrever a posição dos elétrons nos átomos.[2]
Existem quatro números quânticos:
- número quântico principal;
- número quântico de momento angular ou azimutal(secundário);
- número quântico magnético;
- número quântico de spin.
Estes quatro números quânticos, além de se complementarem, nos permitem fazer uma descrição completa dos elétrons nos átomos, pois eles dizem o nível principal de energia do elétron, o subnível de energia, a orientação espacial da nuvem eletrônica e a orientação do próprio elétron na nuvem. Cada combinação dos quatro números quânticos é única para um elétron.
Os primeiros três números quânticos são usados para descrever orbitais atômicos e a caracterização dos elétrons que neles se encontram. O quarto número quântico, número quântico de spin é utilizado na descrição do comportamento específico de cada elétron. Assim, qualquer par de elétrons pode ter até três números quânticos iguais sendo que, neste caso, necessariamente, o quarto número quântico deverá ser diferente, ou seja, este par de elétrons estará ocupando o mesmo orbital sendo que os elétrons apresentam spins opostos.
Número quântico principal, n
O número quântico principal pode tomar como valor qualquer número inteiro positivo. Como o próprio nome o sugere, este número quântico é o mais importante, pois o seu valor define a energia do átomo de hidrogênio (e de outro átomo monoelectrónico de carga nuclear Z) por meio da equação:

onde m e e são a massa dos nêutrons e a carga do elétron, ε0 é a permissividade do vácuo, e h é a constante de Planck. Esta equação foi obtida como resultado da equação de Schrodinger e é desigual a uma das equações obtidas por Bohr, utilizando os seus postulados correctos.
Número quântico de momento angular, l
O número quântico de momento angular, ou azimutal, informa-nos sobre a forma dos orbitais. Como o próprio nome indica, o valor de l define o momento angular do elétron, sendo que o aumento do seu valor implica o aumento correspondente do valor do momento angular. Deste modo, a energia cinética do elétron é associada ao movimento angular e esta dependente da energia total do elétron, pelo que é natural que os valores permitidos de l estejam associados ao número quântico principal. Para um dado valor de n, l pode ter como valores possíveis os números inteiros de 0 a  .
.
 .
.Número quântico magnético, ml
O número quântico magnético especifica a orientação permitida para uma nuvem eletrônica no espaço, sendo que o número de orientações permitidas está diretamente relacionado à forma da nuvem (designada pelo valor de l). Dessa forma, este número quântico pode assumir valores inteiros de -l, passando por zero, até +l.
- l = 0 : corresponde ao subnível s, onde existe somente uma orientação (ml = 0).
- l = 1 : corresponde ao subnível p, onde existem três orientações permitidas, que surgem em decorrência dos três valores de ml (+1, 0, -1). Os três orbitais p são denominados px, py e pz e são orientados de acordo com os três eixos cartesianoss (x, y e z).
- l = 2 : corresponde ao subnível d onde existem cinco orientações permitidas, ou seja, cinco valores de ml (-2, -1, 0, +1, +2). São designados por dz² (orientação coincidente com o eixo z), dx²-y² (orientação coincidente com os eixos x e y, simultaneamente), dxy (orientado entre os eixos x e y), dyz (orientado entre os eixos y e z) e dxz (orientado entre os eixos x e z).
Número quântico de spin, ms[editar | editar código-fonte]
O número quântico de spin são os autovalores possíveis do operador que indica a orientação da fonte extra de momento angular, sem analogia na mecânica clássica, relativa aos elétrons. Existem apenas dois valores possíveis para este número quântico, -1/2 e +1/2.
A tabela a seguir resume os significados de cada número quântico e os valores que eles podem assumir.
| nome | símbolo | significado do orbital | faixa de valores |
|---|---|---|---|
| número quântico principal |  | camada |  |
| número quântico azimutal |  | subnível |  |
| número quântico magnético |  | deslocamento de energia |  |
| número quântico de spin |  | spin |  |
A tabela a seguir mostra a relação entre os números quânticos e os orbitais.
| n | l | Orbital | ml | ms | Número de Combinações |
|---|---|---|---|---|---|
| 1 | 0 | 1s | 0 | -1/2, +1/2 | 2 |
| 2 | 0 | 2s | 0 | -1/2, +1/2 | 2 |
| 2 | 1 | 2p | -1, 0, +1 | -1/2, +1/2 | 6 |
| 3 | 0 | 3s | 0 | -1/2, +1/2 | 2 |
| 3 | 1 | 3p | -1, 0, +1 | -1/2, +1/2 | 6 |
| 3 | 2 | 3d | -2, -1, 0, +1, +2 | -1/2, +1/2 | 10 |
| 4 | 0 | 4s | 0 | -1/2, +1/2 | 2 |
| 4 | 1 | 4p | -1, 0, +1 | -1/2, +1/2 | 6 |
| 4 | 2 | 4d | -2, -1, 0, +1, +2 | -1/2, +1/2 | 10 |
| 4 | 3 | 4f | -3, -2, -1, 0, +1, +2, +3 | -1/2, +1/2 | 14 |
De onde surgem os números quânticos?
Na teoria de Bohr era necessário postular a existência de números quânticos. Contudo, na mecânica quântica, estes números surgem naturalmente da solução matemática da equação de Schrödinger.

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

 (P)
(P)x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Em física atômica, a estrutura fina da raia espectral de um átomo corresponde ao seu desdobramento (separação) em outras linhas de frequências próximas, detectáveis através de um espectroscópio de boa resolução.
Esta estrutura pode ser explicada através da física quântica; devido a quebra parcial da degenerecência de um nível de energia do modelo de Bohr em resultado a três tipos de correções:
- o acomplamento do momento magnético de spin do elétron com campo magnético gerado por seu movimento (momento magnético orbital);
- a consideração do movimento relativístico do elétron;
- O efeito zitterbewegung.
A descoberta da estrutura fina do átomo de hidrogênio concedeu o Nobel de Física à Willis Eugene Lamb em 1955.
Estruturas de nível fino podem ser desdobradas também devido a interação com o momento magnético do núcleo (estrutura hiperfina).
Í
Correção relativística escalar
Classicamente, o termo da energia cinética é:

Entretanto, quando consideramos a relatividade especial, devemos utilizar a forma relativística da energia cinética,

onde o primeiro termo é a energia relativística total, e o segundo termo a energia de repouso do elétron. Expandindo a expressão encontramos:

Então, a correção de primeira ordem ao Hamiltoniano é

Utilizando isso como uma perturbação, podemos calcular as correções de energia de primeira ordem devido aos efeitos relativísticos.

onde  é a função de onda não perturbada. Retornando ao Hamiltoniano não perturbado, vemos que
é a função de onda não perturbada. Retornando ao Hamiltoniano não perturbado, vemos que
 é a função de onda não perturbada. Retornando ao Hamiltoniano não perturbado, vemos que
é a função de onda não perturbada. Retornando ao Hamiltoniano não perturbado, vemos que


Podemos utilizar esse resultado para calcular também a correção relativística:



Para o átomo de hidrogênio,  ,
,  , and
, and  onde
onde  é o raio de Bohr,
é o raio de Bohr,  é o número quântico principal e
é o número quântico principal e  é o número quântico azimutal. Assim, a correção para o átomo de hidrogênio é
é o número quântico azimutal. Assim, a correção para o átomo de hidrogênio é
 ,
,  , and
, and  onde
onde  é o raio de Bohr,
é o raio de Bohr,  é o número quântico principal e
é o número quântico principal e  é o número quântico azimutal. Assim, a correção para o átomo de hidrogênio é
é o número quântico azimutal. Assim, a correção para o átomo de hidrogênio é
A interação de spin-Órbita (Mecânica Quântica)
Na inclusão introdutória do spin na função de onda de Schrodinger, supõe-se que as coordenadas do spin são independentes das coordenadas do espaço de configuração.[1]
Assim, a função de onda total é escrita como uma função de produto.

 (P)
(P)A suposição feita acima implica que não existe interação entre L e S, i.e 

Neste caso,  é uma auto-função de ambos
é uma auto-função de ambos  e
e  e portanto
e portanto  e
e  são bons números quânticos; em outras palavras, as projeções de
são bons números quânticos; em outras palavras, as projeções de  e
e  são constantes do movimento.
são constantes do movimento.
 é uma auto-função de ambos
é uma auto-função de ambos  e
e  e portanto
e portanto  e
e  são bons números quânticos; em outras palavras, as projeções de
são bons números quânticos; em outras palavras, as projeções de  e
e  são constantes do movimento.
são constantes do movimento.Mas na verdade existe uma interação entre  e
e  chamada interação Spin-Órbita expressa em termos da grandeza
chamada interação Spin-Órbita expressa em termos da grandeza  .
.
 e
e  chamada interação Spin-Órbita expressa em termos da grandeza
chamada interação Spin-Órbita expressa em termos da grandeza  .
.Dado que  não comuta quer com
não comuta quer com  ou com
ou com  , a equação (P) torna-se incorreta e
, a equação (P) torna-se incorreta e  e
e  deixam de ser bons números quânticos.
deixam de ser bons números quânticos.
 não comuta quer com
não comuta quer com  ou com
ou com  , a equação (P) torna-se incorreta e
, a equação (P) torna-se incorreta e  e
e  deixam de ser bons números quânticos.
deixam de ser bons números quânticos. Nós imaginamos a interação spin-órbita como o momento magnético spin estacionária interagindo com o campo magnético produzido pelo núcleo orbitante.
No sistema de referência de repouso do electrão, há um campo eléctrico

Onde  dirige‐se do núcleo em direção ao electrão.
dirige‐se do núcleo em direção ao electrão.
 dirige‐se do núcleo em direção ao electrão.
dirige‐se do núcleo em direção ao electrão. Assumindo que  é a velocidade do electrão no sistema de referência de repouso do núcleo, a corrente produzida pelo movimento nuclear é:
é a velocidade do electrão no sistema de referência de repouso do núcleo, a corrente produzida pelo movimento nuclear é:
 é a velocidade do electrão no sistema de referência de repouso do núcleo, a corrente produzida pelo movimento nuclear é:
é a velocidade do electrão no sistema de referência de repouso do núcleo, a corrente produzida pelo movimento nuclear é: 
No sistema de referência de repouso do electrão.
Portanto

O momento de spin do electrão realiza um movimento precessional neste campo com frequência de Larmor:

Com energia potencial

As equações acima são válidas no quadro de referência de repouso electrão.
A Transformação para o sistema de referência de repouso do núcleo introduz um fator de ½ - chamado o fator de Thomas. [Isto pode ser mostrado, calculando o tempo dilatado entre os dois sistemas de referência em repouso].[1]
Portanto, um observador no sistema de referência de repouso do núcleo poderia observar o electrão a realizar um movimento de precessão com uma velocidade angular de
 (T)
(T)e por uma energia adicional dada por

As duas Eqs acima podem ser colocadas em uma forma mais geral, restringindo o V ser qualquer potencial central com simetria esférica.
De forma que

e então

A equação (T) torna-se então

E a energia adicional

O produto escalar

Para spin = ½

A separação energética se torna então

Para o potencial de Coulomb a separação energética pode ser aproximada por:

Onde  é o comprimento de onda de Compton
é o comprimento de onda de Compton
 é o comprimento de onda de Compton
é o comprimento de onda de Compton ou
ou 
Um resultado útil no cálculo é citado sem prova. O valor médio de  i.e.
i.e.
 i.e.
i.e.
para 

De modo que a separação energética se torna

para 

as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.

x

 = entropia reversível
= entropia reversível

x

 = entropia reversível
= entropia reversível


x

 = entropia reversível
= entropia reversível



tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Orbital atômico e número quântico + entropia no sistema decadimensional e categorial Graceli.
sexta-feira, 25 de janeiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D


x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Orbitais atômicos (português brasileiro) ou orbitais atómicas (português europeu) de um átomo, é a denominação dos estados estacionários da função de onda de um elétron (funções próprias do Hamiltoniano (H) na equação de Schrödinger  , onde
, onde  é a função de onda).[1] Entretanto, os orbitais não representam a posição exata do elétron no espaço, que não pode ser determinada devido à sua natureza ondulatória; apenas delimitam uma região do espaço na qual a probabilidade de encontrar o elétron é mais alta. [2]
é a função de onda).[1] Entretanto, os orbitais não representam a posição exata do elétron no espaço, que não pode ser determinada devido à sua natureza ondulatória; apenas delimitam uma região do espaço na qual a probabilidade de encontrar o elétron é mais alta. [2]
 , onde
, onde  é a função de onda).[1] Entretanto, os orbitais não representam a posição exata do elétron no espaço, que não pode ser determinada devido à sua natureza ondulatória; apenas delimitam uma região do espaço na qual a probabilidade de encontrar o elétron é mais alta. [2]
é a função de onda).[1] Entretanto, os orbitais não representam a posição exata do elétron no espaço, que não pode ser determinada devido à sua natureza ondulatória; apenas delimitam uma região do espaço na qual a probabilidade de encontrar o elétron é mais alta. [2]Números quânticos
- O valor do número quântico
(número quântico principal ou primário, que apresenta os valores
[também representado por
]) define o tamanho do orbital. Quanto maior o número, maior o volume do orbital. Também é o número quântico que tem a maior influência na energia do orbital.
- O valor do número quântico
(número quântico secundário ou azimutal, que apresenta os valores
) indica a forma do orbital e o seu momento angular. O momento angular é determinado pela equação:
A notação científica (procedente da espectroscopia) é a seguinte:
, orbitais
, orbitais
, orbitais
, orbitais
Para os demais orbitais segue-se a ordem alfabética.
- O valor do
(número quântico terciário ou magnético, que pode assumir os valores
) define a orientação espacial do orbital diante de um campo magnético externo. Para a projeção do momento angular diante de um campo externo, verifica-se através da equação:
- O valor de
(número quântico magnético de spin ou spin) pode ser
. O valor de
que equivale a uma valor fixo
.
Pode-se decompor a função de onda empregando-se o sistema de coordenadas esféricas da seguinte forma:
Onde
representa a distância do elétron até o núcleo, e
a geometria do orbital.
Para a representação do orbital emprega-se a função quadrada, 
 , já que esta é proporcional à densidade de carga e, portanto, a densidade de probabilidade, isto é, o volume que encerra a maior parte da probabilidade de encontrar o elétron ou, se preferir, o volume ou a região do espaço na qual o elétron passa a maior parte do tempo.
, já que esta é proporcional à densidade de carga e, portanto, a densidade de probabilidade, isto é, o volume que encerra a maior parte da probabilidade de encontrar o elétron ou, se preferir, o volume ou a região do espaço na qual o elétron passa a maior parte do tempo.

 , já que esta é proporcional à densidade de carga e, portanto, a densidade de probabilidade, isto é, o volume que encerra a maior parte da probabilidade de encontrar o elétron ou, se preferir, o volume ou a região do espaço na qual o elétron passa a maior parte do tempo.
, já que esta é proporcional à densidade de carga e, portanto, a densidade de probabilidade, isto é, o volume que encerra a maior parte da probabilidade de encontrar o elétron ou, se preferir, o volume ou a região do espaço na qual o elétron passa a maior parte do tempo.Orbital s[editar | editar código-fonte]
O orbital  tem simetria esférica ao redor do núcleo. Na figura seguinte, são mostradas duas alternativas de representar a nuvem eletrônica de um orbital
tem simetria esférica ao redor do núcleo. Na figura seguinte, são mostradas duas alternativas de representar a nuvem eletrônica de um orbital  :
:
 tem simetria esférica ao redor do núcleo. Na figura seguinte, são mostradas duas alternativas de representar a nuvem eletrônica de um orbital
tem simetria esférica ao redor do núcleo. Na figura seguinte, são mostradas duas alternativas de representar a nuvem eletrônica de um orbital  :
:- Na primeira, a probabilidade de encontrar o elétron (representada pela densidade de pontos) diminui à medida que nos afastamos do núcleo.
- Na segunda, se apresenta o volume esférico no qual o elétron passa a maior parte do tempo.
Pela simplicidade, a segunda forma é mais utilizada.
Para valores de número quântico principal maiores que um, a função densidade eletrônica apresenta  nós, nos quais a probabilidade tende a zero. Nestes casos, a probabilidade de encontrar o elétron se concentra a certa distância do núcleo.
nós, nos quais a probabilidade tende a zero. Nestes casos, a probabilidade de encontrar o elétron se concentra a certa distância do núcleo.
 nós, nos quais a probabilidade tende a zero. Nestes casos, a probabilidade de encontrar o elétron se concentra a certa distância do núcleo.
nós, nos quais a probabilidade tende a zero. Nestes casos, a probabilidade de encontrar o elétron se concentra a certa distância do núcleo.
Orbital p[editar | editar código-fonte]
A forma geométrica dos orbitais  é a de duas esferas achatadas até o ponto de contato (o núcleo atómico) e orientadas segundo os eixos de coordenadas. Em função dos valores que pode assumir o terceiro número quântico
é a de duas esferas achatadas até o ponto de contato (o núcleo atómico) e orientadas segundo os eixos de coordenadas. Em função dos valores que pode assumir o terceiro número quântico  , obtém-se três orbitais
, obtém-se três orbitais  simétricos, orientados segundo os eixos
simétricos, orientados segundo os eixos  . De maneira análoga ao caso anterior, os orbitais
. De maneira análoga ao caso anterior, os orbitais  apresentam
apresentam  nós radiais na densidade eletrónica, de modo que, à medida que aumenta o valor do número quântico principal, a probabilidade de encontrar o elétron afasta-se do núcleo atômico.
nós radiais na densidade eletrónica, de modo que, à medida que aumenta o valor do número quântico principal, a probabilidade de encontrar o elétron afasta-se do núcleo atômico.
 é a de duas esferas achatadas até o ponto de contato (o núcleo atómico) e orientadas segundo os eixos de coordenadas. Em função dos valores que pode assumir o terceiro número quântico
é a de duas esferas achatadas até o ponto de contato (o núcleo atómico) e orientadas segundo os eixos de coordenadas. Em função dos valores que pode assumir o terceiro número quântico  , obtém-se três orbitais
, obtém-se três orbitais  simétricos, orientados segundo os eixos
simétricos, orientados segundo os eixos  . De maneira análoga ao caso anterior, os orbitais
. De maneira análoga ao caso anterior, os orbitais  apresentam
apresentam  nós radiais na densidade eletrónica, de modo que, à medida que aumenta o valor do número quântico principal, a probabilidade de encontrar o elétron afasta-se do núcleo atômico.
nós radiais na densidade eletrónica, de modo que, à medida que aumenta o valor do número quântico principal, a probabilidade de encontrar o elétron afasta-se do núcleo atômico.
Orbital d[editar | editar código-fonte]
Os orbitais  tem uma forma mais diversificada: quatro deles têm forma de 4 lóbulos de sinais alternados (dois planos nodais, em diferentes orientações espaciais), e o último é um duplo lóbulo rodeado por um anel (um duplo cone nodal). Seguindo a mesma tendência, apresentam
tem uma forma mais diversificada: quatro deles têm forma de 4 lóbulos de sinais alternados (dois planos nodais, em diferentes orientações espaciais), e o último é um duplo lóbulo rodeado por um anel (um duplo cone nodal). Seguindo a mesma tendência, apresentam  nós radiais.
nós radiais.
 tem uma forma mais diversificada: quatro deles têm forma de 4 lóbulos de sinais alternados (dois planos nodais, em diferentes orientações espaciais), e o último é um duplo lóbulo rodeado por um anel (um duplo cone nodal). Seguindo a mesma tendência, apresentam
tem uma forma mais diversificada: quatro deles têm forma de 4 lóbulos de sinais alternados (dois planos nodais, em diferentes orientações espaciais), e o último é um duplo lóbulo rodeado por um anel (um duplo cone nodal). Seguindo a mesma tendência, apresentam  nós radiais.
nós radiais.
Estadologia Graceli – 4. E princípio entrópico tempo / instabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.


 = entropia reversível
= entropia reversível

tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Nível de energia + ENTROPIA QUÂNTICA no SDC GRACELI
terça-feira, 29 de janeiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Em mecânica quântica, nível de energia ou nível energético é um estado quântico (de um elétron, átomoou molécula, por exemplo) cuja energia está bem definida ao longo do tempo. Desse modo, os níveis energéticos são as funções próprias do operador hamiltoniano, e suas energias respectivas são seus valores.[1]
As diferentes espectroscopias estudam as transições entre os diferentes níveis de energia. A espectroscopia infravermelha, por exemplo, estuda transições entre os níveis energéticos da vibração molecular, a espectroscopia ultravioleta e visível estuda as transições eletrônicas e a espectroscopia Mössbauer se ocupa das transições nucleares.[2]
Na química e na física atômica, uma camada eletrônica, ou um nível de energia principal, pode ser pensado como uma órbita de elétrons girando ao redor do núcleo do átomo. A camada mais próxima do núcleo é chamada de "camada 1" (também chamada de "camada K"), seguida da" camada 2" (ou "camada L"), depois a "camada 3" (ou "camada M"), e assim por diante, conforme se afasta do núcleo. As camadas correspondem aos números quânticos principais (n = 1,2,3,4...) ou são nomeadas na ordem alfabética com letras usadas na rotação de raio-x (K, L, M,...).
Se a energia potencial é considerada zero a uma distância infinita do núcleo do átomo ou da molécula, convenção usual, então os respectivos estados eletrônicos possuem energia potencial negativa.
Se um átomo, íon ou molécula está no menor estado possível de energia, ele e seus elétrons são ditos no estado fundamental. Se ele está em um nível mais alto de energia, é dito excitado, ou quaisquer elétrons que possuem energia maior do que o estado fundamental estão excitados. Se mais de um estado mecânico quântico está com a mesma energia, os níveis de energia estão "degenerados". Eles são então chamados de níveis de energia degenerados.[3]
Estados quantizados de energia resultam de uma relação entre a energia de uma partícula e o seu comprimento de onda. Para uma partícula confinada, como um elétron em um átomo, a função de onda tem a forma de ondas estacionárias. Apenas estados estacionários com energia correspondente a um número inteiro de comprimentos de onda podem existir; para outros estados as ondas interferem destrutivamente, resultando em probabilidade de densidade igual a zero. Exemplos elementares que mostram matematicamente como níveis de energia acontecem são a partícula em uma caixa e o oscilador harmônico quântico. O elétron é uma partícula subatômica fundamental que carrega uma carga elétrica negativa.[3]
História[editar | editar código-fonte]
A primeira evidência da quantização em átomos foi a observação de linhas espectrais na luz vinda do sol em cerca de 1800 por Joseph von Fraunhofer e William Hyde Wollaston. A noção de níveis de energia foi proposta em 1913 pelo físico dinamarquês Niels Bohr na Teoria de Bohr para o átomo. A teoria da mecânica quântica moderna, dando a explicação desses níveis de energia em termos da equação de Schrödinger, foi desenvolvida por Erwin Schrödinger e Werner Heisenberg em 1926.[3]
Transição de Níveis de Energia[editar | editar código-fonte]
Elétrons em átomos e moléculas podem trocar (fazer transição) de níveis de energia ao emitirem ou absorverem um fóton, ou radiação eletromagnética, tal energia deve ser exatamente igual à diferença energética entre os dois níveis. Elétrons podem também ser completamente removidos de uma espécie química, como um átomo, molécula, ou íon. A remoção completa de um elétron de um átomo pode ser uma forma de ionização, que é efetivamente mover o elétron para um orbital com um número quântico principal infinito, tão longe de forma a praticamente não ter efeito algum sobre o átomo remanescente (íon). Para vários tipos de átomos, existem a 1ª, 2ª, 3ª energia de ionização e assim por diante, que podem ser fornecidas ao átomo em estado fundamental para remover elétrons do menor ao maior nível de energia. Energia em quantidades opostas também pode ser liberada, muitas vezes em forma de energia fotoelétrica, quando elétrons entram em contato com ións positivamente carregados (ou átomos). Moléculas também podem passar por transições em seus níveis de energia vibracionais e rotacionais. A transição de nível de energia também pode ser não-radioativa, significando que não ocorre a emissão ou absorção de um fóton.
Se um átomo, íon ou molécula está no menor nível de energia possível, ele e seus elétrons são ditos em estado fundamental. Se estão no maior nível de energia, são ditos excitados, ou qualquer elétron possui uma energia maior que o estado fundamental está excitado. Tal espécie pode ser excitada a um nível de energia maior ao absorver um fóton cuja energia é igual a diferença de energia entre dois níveis. Por outro lado, uma espécie pode ir para um nível de energia inferior ao emitir espontaneamente um fóton com energia igual a diferença energética. A energia de um fóton é igual a constante de Plank (h) vezes a sua frequência (f) e, portanto, é proporcional a sua frequência, ou inversamente proporcional ao seu comprimento de onda (λ).

Estadologia Graceli – 4. E princípio entrópico tempo / instabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Postado por cientista e filósofo Ancelmo Luiz Graceli às 01:11
Assinar: Postagens (Atom)
Postado por cientista e filósofo Ancelmo Luiz Graceli às 01:11
Assinar: Postagens (Atom)
Postado por cientista e filósofo Ancelmo Luiz Graceli às 01:11
Assinar: Postagens (Atom)
Tema Simples. Tecnologia do Blogger.Postado por cientista e filósofo Ancelmo Luiz Graceli às 01:11
Assinar: Postagens (Atom)
Tema Simples. Tecnologia do Blogger.tado por cientista e filósofo Ancelmo Luiz Graceli às 01:11
Assinar: Postagens (Atom)
Postado por cientista e filósofo Ancelmo Luiz Graceli às 01:11
Assinar: Postagens (Atom)
Postado por cientista e filósofo Ancelmo Luiz Graceli às 01:11
Assinar: Postagens (Atom)
- Gerar link
- X
- Outros aplicativos











![{\displaystyle \chi _{S}:\left\{{\begin{matrix}|++\rangle \qquad [\mathbf {s} _{z}=1]\\{\frac {1}{\sqrt {2}}}(|+-\rangle +|-+\rangle )\quad [\mathbf {s} _{z}=0]\\|--\rangle \qquad [\mathbf {s} _{z}=-1]\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d2db165f867e48e9549581259fa1570eebd273e)
![{\displaystyle \chi _{A}:{\frac {1}{\sqrt {2}}}(|+-\rangle -|-+\rangle )\quad [\mathbf {s} _{z}=0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2424271b35dc397ae935afa545f5227dc7961d42)










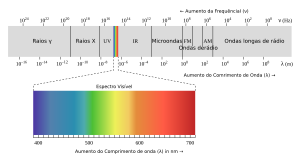



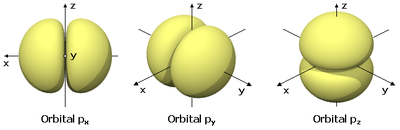
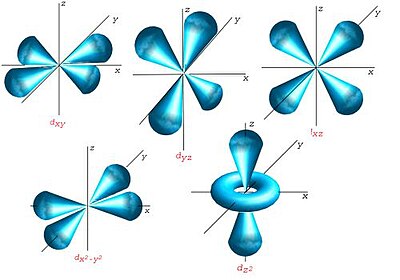






Comentários
Postar um comentário